这个文章首次提出了基于RNN Encoder-Decoder框架的NMT模型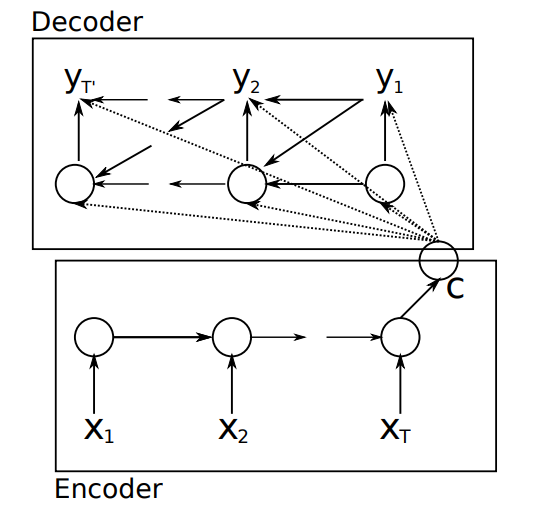
RNN Encoder-Decoder
1 Encoder
首先将源句子的每个词转换为500维的词向量\(e(x_i)\in R^{500}\),encoder使用GRU,hidden units为1000,在每一个时刻有hidden state
$$h_j^{< t >}=z_jh_j^{< t-1 >}+(1-z_j)\hat h_j^{< t >}$$
其中
$$\hat h_j^{< t >}=tanh([\mathbf We(x_t)]_j+[\mathbf U(\mathbf r\odot \mathbf h_{< t-1 >})]_j)$$ $$z_j=\sigma([\mathbf W_ze(x_t)]_j]+[\mathbf U_z\mathbf h_{< t-1 >}]_j)$$ $$r_j=\sigma([\mathbf W_re(x_t)]_j)+[\mathbf U_r\mathbf h_{< t-1 >}]_j)$$
在最后一个step计算完\(h\)之后,源句子的信息表示\(c\)为
$$\mathbf c=tanh(\mathbf V\mathbf h^{< N >})$$
2 Decoder
deocder的hidden state可以用这个初始化
$$\mathbf h’^0=tanh(\mathbf V’\mathbf c)$$
那么对于每个step的hidden state,可以由以下公式得到
$$h_j’^{< t >}=z_j’h_j’^{< t-1 >}+(1-z_j)\hat h_j’^{< t >}$$
其中
$$\hat h_j’^{< t >}=tanh([\mathbf W’e(y_{t-1})]_j+[\mathbf U\mathbf {h_{< t-1 >}]_j+Cc}])$$ $$z_j’=\sigma([\mathbf W’_ze(y_{t-1})]_j]+[\mathbf U’_z\mathbf h’_{< t-1 >}]_j+\mathbf {[C_zc]_j})$$ $$r_j’=\sigma([\mathbf W’_re(y_{t-1})]_j)+[\mathbf U’_r\mathbf h’_{< t-1 >}]_j+\mathbf {[C_rc]_j})$$
\(e(y_0)\)是一个全0向量,与encoder类似下\(e(y)\)是词向量.encoder是将句子编码,decoder不一样,它要生成句子,在每一个time \(t\),decoder生成第\(j\)个词的方法为
$$p(y_{t,j}=1|y_{t-1},…,y_1,X)=\frac {exp(g_js_{< t >})}{\sum_{j’=1}^Kexp(g_{j’}s_{< t >})}$$
其中
$$s_i^{< t >}=max\lbrace s_{2i-1}’^{< t >},s_{2i}’^{< t >}\rbrace $$ $$s’^{< t >}=\mathbf {O_hh’^{< t >}+o_yy_{t-1}+o_cc}$$
\(s_i^{< t >}\)可以看作是一个\(maxout\).为了计算效率,将一个的输出权重矩阵\(\mathbf G\)替换为两个矩阵的点乘
$$\mathbf {G=G_lG_r}$$
链接
论文 Learning Phrase Representations using RNN Encoder–Decoder for Statistical
注释
所有数据,图表均来源于论文.